東大2004年問2整数問題を使ってアプローチの仕方を考えてみた
こんなTweetをみかけたので、本当かな?って考えてみた。
問題はこちら

そしてエクセルを使って実験をしてみました。
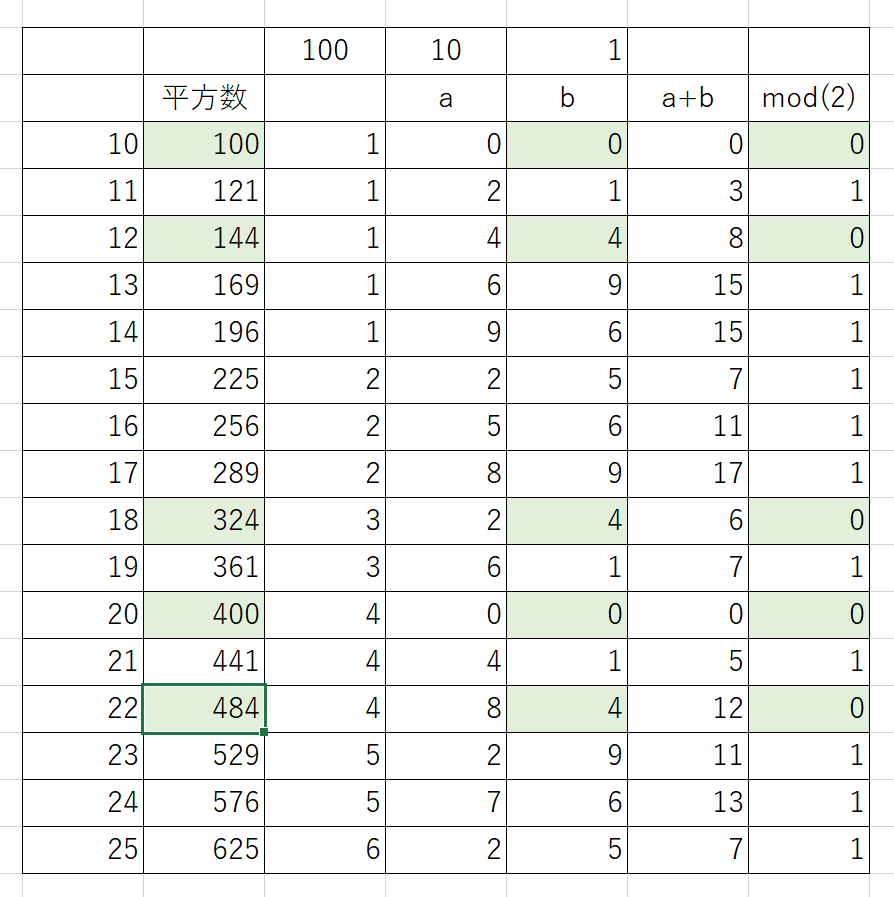
たしかにa+bが偶数になっていたらbは0か4になっています。
ではなぜそうなるんだろうかとこの実験の結果を使いながら考えてみます。
いきなり平方数の下2桁を考えるのは大変なので、2乗する前の整数をnとして
n = 100p + 10q + r (p は非負整数, q, r は 1 桁の整数) で考えます。
n^2 = (100 の倍数) + 20qr + r^2
n^2の下2桁は、
一の位b:r^2の一の位と一致
十の位a:20qr+r^2の十の位と一致
(たとえば14の2乗は一の位が6、十の位が20×1×4+4^2=96から9)
十の位の20qrは20の倍数なので必ず偶数となる。
n^2の下2桁a,bの和が偶数になるには、偶+偶か奇+奇でr^2の各位の偶奇が一致する必要がある。(20qr は a + b の偶奇に影響しない)
この条件を満たす2桁以下の平方数は、
00,01,04,09,16,25,36,49,64,81のうち00, 04, 64の3つしかない。
bすなわちr^2の一の位は必ず0か4と言える。
(2)は
下4桁が全部同じ数字なので、下2桁の和は当然偶数になります。
ということは、平方数の下2桁を考えると00,21,44,69,96,25,56,89,24,61のうち下4桁としてありうる数字は、0000か4444しかないことが分かる。
よって4444のケースが不適なことが言えれば証明できたことになります。
4444のケースを排除するには、背理法を使います。
M^2 =10000m+4444 = 4×(2500m+1111)と仮定すると、
Mが整数となるので 2500m+1111 が平方数でないといけません。
ところが2500m+1111の下2桁は11なので(1)から平方数になりえません。
これで矛盾が発生したので背理法成立です。
(1)(2)が見事に連動していました。

